Un LLM expliqué en mots de tous les jours

Un grand modèle de langage (LLM) est un système d’intelligence artificielle dont le but est de générer du texte en analysant les relations entre les mots. Certains LLM, comme GPT par exemple, sont entraînés à prédire le mot suivant dans une phrase. Un LLM est « entraîné » sur une grande masse de données (textes issus de livres, articles, etc.) afin d’apprendre les relations implicites entre les mots. Au cours de cette phase d’entraînement, le modèle prédit le prochain mot, confronte sa prédiction à la réalité et ajuste les liens implicites qu’il perçoit entre les mots en modifiant les probabilités qu’il attribue à chaque mot de survenir dans chaque contexte. Par exemple, si on lui donne la phrase « Aujourd’hui, il fait beau et le ciel est… », il tente une prédiction « rouge », puis progresse jusqu’à prédire que « bleu » est le mot suivant le plus probable en se basant sur les milliers de phrases similaires qu’il a vues auparavant.

Les données textuelles qui sont fournies au LLM pour son entraînement doivent être préparées pour être insérées dans les modèles mathématiques utilisés. Chaque phrase est pour cela découpée en unités appelées tokens, qui peuvent être des fragments de mots, des sous-mots, des mots entiers parfois, voire des caractères individuels selon la méthode utilisée. Ces tokens sont l’équivalent de l’alphabet pour chaque modèle : ce sont les briques élémentaires utilisées par un LLM pour traiter le language naturel, c’est-à-dire le nôtre. Les tokens sont ensuite transformés en représentations numériques. Ces valeurs permettent d’exprimer des liens entre les mots : par exemple, le mot « maladie » et le mot « hôpital » auront un score proche pour indiquer leur proximité conceptuelle. Il est en effet probable que l’un et l’autre apparaissent dans le même contexte.

A partir du contexte, qui est initialement constitué de la question d’un utilisateur par exemple, le modèle applique une probabilité pour générer le prochain mot. Ce mot rejoint ensuite le contexte et lui permet de générer un mot suivant. Et ainsi de suite jusqu’à créer un texte de longueur désirée. Dans l’exemple précédent, « bleu » rejoint le nouveau contexte, et le modèle prédit le mot suivant sur cette base, et ainsi de suite, jusqu’à ce que la limite désirée soit atteinte. Son fonctionnement repose donc uniquement sur une analyse probabiliste et pas sur une compréhension, au sens humain, des sujets traités.

C’est là l’une de leurs limites, soulignée par le chercheur Yann Lecun pour qui les LLM « ne comprennent pas la réalité sous-jacente aux concepts qu’ils manipulent« . Ils se contentent d’appliquer des probabilités apprises sur des données énormes lors de la phase d’entraînement. Leur grande éloquence leur donne une apparence d’intelligence mais elle n’est que superficielle : ils restituent des contenus qui sont, eux, intelligents en moyenne (si la qualité des données d’entraînement est bonne). Il s’agit en résumé de répétitions intelligemment (ou plutôt statistiquement) adaptées au contexte. Mais le LLM ne s’appuie par sur un raisonnement logique de type humain.

Un LLM expliqué en concepts plus avancés

Un LLM est un réseau de neurones profond entraîné à apprendre la distribution conditionnelle de probabilité sur le vocabulaire (les mots que le modèle a appris). Autrement dit, quel(s) mot(s) ont le plus de chance d’apparaître après une séquence donnée de mots (le contexte).

Tokenisation et embedding

Les données sont préparées pour qu’elles puissent être traitées par le réseau : c’est la phase de tokenisation, qui a donc lieu avant l’entrée dans le réseau neuronal. Chaque phrase est décomposée en tokens, de taille possiblement inférieure à un mot. Par exemple, la phrase « Comprendre est utile » sera transformée en une suite d’indices numériques [1234, 567, 890].

Avant leur entrée dans le réseau, les indices sont ensuite transformés en vecteurs continus qui permettent de représenter numériquement les liens existants entre chaque mot (relations sémantiques, syntaxiques, contextuelles – autant de dimensions que souhaité). C’est la phase d’embedding. Dans cet espace multi-dimensionnel, plus les coordonnées de chaque mot sont proches, c’est-à-dire plus ils sont proches au sein de cet espace, plus ils sont semblables et donc susceptibles d’apparaître ensemble dans une même phrase, un même paragraphe. Par exemple :
maladie → [0.9, -0.2, 0.5]
hôpital → [0.8, -0.1, 0.6]
chien → [-0.3, 0.5, -0.9]
Cet embedding indique que les mots « maladie » et « hôpital » sont proches, alors que « chien » est plus éloigné.

Les réseaux neuronaux et l’apprentissage profond

Un réseau neuronal reçoit des données (couche d’entrée), les transforme au sein des couches cachées et produit un résultat dans la couche de sortie. Il transmet ensuite le signal aux neurones suivants. Plus le réseau contient de couches cachées, plus il est profond et capable d’apprendre des relations complexes.

Le but de tout réseau neuronal, utilisé dans le cadre d’un LLM ou non, est de modéliser les relations qui existent entre les données. Il s’agit donc de découvrir une fonction f qui doit correspondre le mieux possible aux données. Plus concrètement, un neurone applique une fonction f au vecteur d’entrée $$\mathbf{x} = (x_1, x_2, \dots, x_n) $$ pour produire une sortie y, définie comme :
$$y = f(\mathbf{x}) = \sigma \left( \mathbf{w}^T \mathbf{x} + b \right)$$ Pour découvrir (apprendre !) la fonction f, l’idée est de trouver les poids w et les biais b pour que la fonction approxime les données avec l’erreur la plus faible.

Dans notre cas, quelle fonction un LLM cherche-t-il à apprendre grâce au réseau neuronal ? Son but est de deviner le prochain mot d’une séquence de mots existants : il doit donc apprendre une distribution de probabilité conditionnelle, la probabilité que le mot suivant soit le mot ω n sachant que les mots précédents étaient les mots ω_1 à ω_n-1 (ce qu’on appelle le contexte).

Une fonction de perte L mesure l’écart entre la sortie du réseau (prédiction) et les valeurs réelles attendues. Pour un LLM, la fonction de perte la plus couramment utilisée est l’entropie croisée (CrossEntropyLoss) qui compare la distribution prédite avec la distribution réelle.

En résumé, le réseau de neurones reçoit un signal : le contexte, composé des tokens des mots précédents (éventuellement des mots suivants dans certains cas); il s’agit de la couche d’entrée. Au sein des couches cachées, le LLM apprend la probabilité conditionnelle. Lors de cette phase d’entraînement, il ajuste les poids de son modèle afin de former une prédiction (le mot suivant) le plus proche possible de la réalité, c’est-à-dire de ses données d’entraînement. Une fois entraîné, il est prêt à répondre aux questions des utilisateurs : il appliquera alors la distribution de probabilité conditionnelle qu’il a apprise.

Un réseau de neurones profonds peut présenter différentes architectures : en particulier les réseaux de neurones récurrents (RNN) et les transformers. L’ancienne génération de LLM reposait sur les RNN qui traitaient les mots un par un et étaient sensibles à l’ordre de la séquence des mots. Depuis 2017, les transformers ont supplanté les RNN : grâce au principe d’attention, l’importance des mots est pondérée sans se limiter à leur seule position dans la séquence et donc à un traitement séquentiel.

Ancienne génération de LLM : réseaux neuronaux récurrents

Dans un RNN, les prédictions sont établies en fonction des mots précédents intégrés de façon séquentielle. Les mots les plus proches ont plus de poids : le mot n-1 aura un poids bien supérieur au premier mot de la séquence, surtout si elle est longue.

Le LLM cherche à apprendre la probabilité conditionnelle suivante : $$P(w_n | w_1, w_2, …, w_{n-1})$$

La fonction de perte (entre la distribution estimée et la distribution réelle) est minimisée (par exemple) par la méthode de descente des gradients : les poids sont ajustés dans la direction qui réduit l’erreur. La direction à suivre est indiquée par la dérivée de la fonction de perte en fonction des poids. En simplifiant, les nouveaux poids sont donc ajustés ainsi : $$w = w – \eta \frac{\partial L}{\partial w}$$ où le paramètre η est le taux d’apprentissage qui contrôle l’ampleur de la mise à jour. Pour reprendre une image classique, imaginons que nous sommes au sommet d’une colline, l’erreur actuelle, et que nous souhaitons atteindre la vallée rapidement (le minimum de l’erreur). La descente de gradient consiste à choisir la pente optimale en utilisant la dérivée pour indiquer la direction à suivre.

Les réseaux de neurones récurrents souffrent de plusieurs inconvénients, parmi lesquels, la difficulté à capter des dépendances entre mots éloignés, le problème des gradients évanescents et le traitement séquentiel qui ralentissait l’entraînement.

Mécanisme d’attention et transformers : génération plus récente de LLM

Le mécanisme d’attention a été développé dans l’article Attention Is All You Need (Vaswani et al, 2017) donnant naissance aux transformers. Un transformer n’analyse pas séquentiellement les mots précédents comme le fait un RNN : il leur attribue des importances variables. Le premier mot, le plus éloigné, pourrait donc tout à fait avoir un poids bien plus important que le (n-1)-ième, à la différence des RNN où le (n-1)-ième mot est implicitement le plus important.

Ainsi, contrairement à un modèle RNN, où la probabilité conditionnelle dépend directement des mots précédents, la transformer apprend une représentation abstraite du contexte. Il n’apprend pas directement $$P(w_n \mid w_1, w_2, \ldots, w_{n-1})$$ mais plutôt : $$ P(w_n \mid \mathbf{c}(w_1, w_2, \ldots, w_{n-1})) $$ où c est une fonction non linéaire qui transforme l’embedding initial en une représentation optimisée. Cette représentation consiste à attribuer des importances différentes aux mots de la séquence, indépendamment de leur place au sein de celle-ci.

Pourquoi parler d’ »attention » ? Parce que le LLM cherche à apprendre l’attention optimale, l’importance, à accorder à chaque mot de la séquence pour établir sa prédiction. Et ce, au-delà donc de leur simple position dans la séquence. Ainsi, plutôt que de considérer uniquement les mots du contexte de façon linéaire comme avec un RNN, le modèle apprend à pondérer l’importance de chacun d’entre eux.

Dans un transformer, le mot « comprendre » est représenté par son embedding initial, modifié dynamiquement par les mécanismes d’attention qui ajustent son poids relatif par rapport aux autres mots de la phrase. L’interprétation devient contextuelle et donc dynamique. Cela permet de saisir des dépendances entre des mots éloignés au sein de la phrase considérée. Et aussi de lever certaines ambigüités, car les poids ne sont plus constants mais dépendent désormais du contexte. Par exemple, le mot « puce » sera interprété différemment si les mots « ordinateur », « processeurs » apparaissent, ou si les mots « chien », « démangeaison » apparaissent, donc selon le contexte.

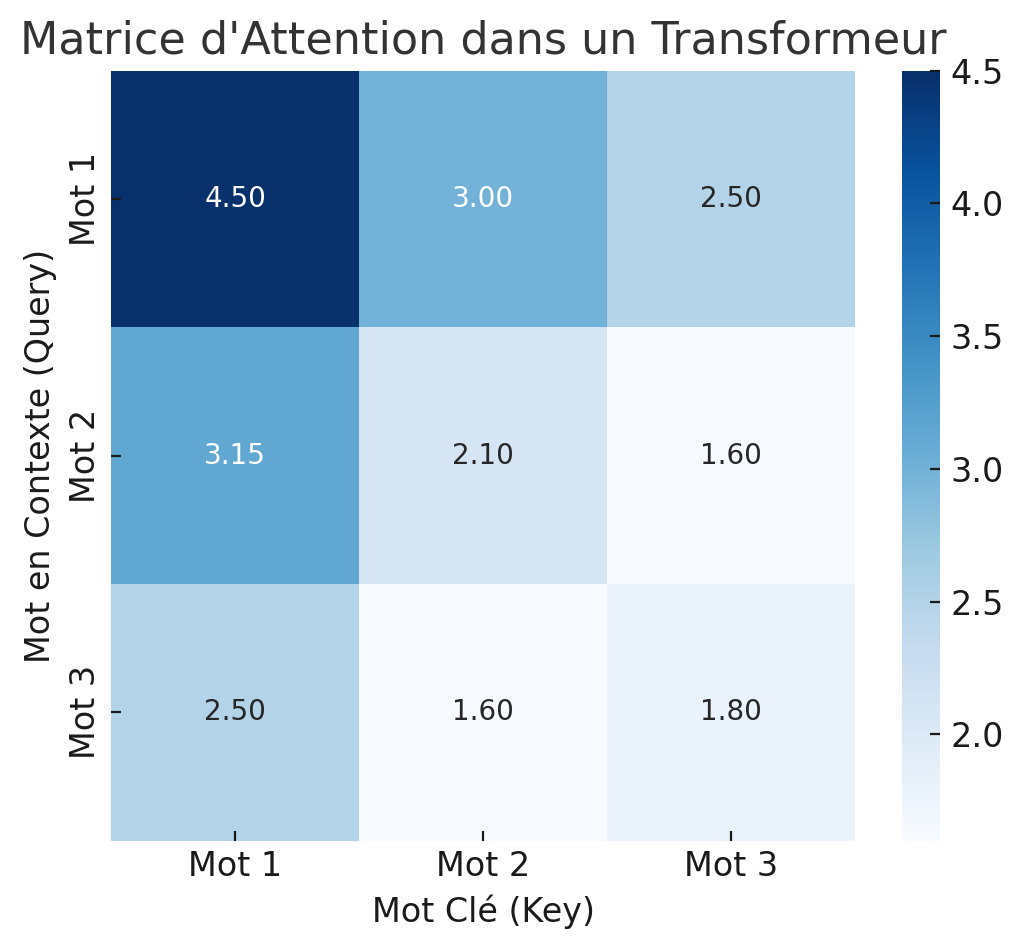
On calcule d’abord un score d’attention : l’attention que le mot i doit accorder au mot j : $$\text{Score}_{i,j} = Q_i \cdot K_j^T$$. Q_i (query) est une projection linéaire de l’embedding initial du mot analysé (qui est transformé par une matrice de poids W_Q), et K_j (key) une projection linéaire de l’embedding initial du mot j (le contexte) (transformé par une matrice de poids W_K). Le produit $$ Q K^T $$ génère une matrice d’attention où chaque élément (i,j) correspond au score d’attention entre le mot i et le mot j. Si pour analyser un mot donné, il faut particulièrement attention à un autre mot, alors leurs vecteurs seront proches, donc leur produit scalaire sera grand. Si la matrice d’attention obtenue est :
$$\begin{bmatrix} 4.5 & 3.0 & 2.5 \\ 3.15 & 2.1 & 1.6 \\ 2.52 & 1.68 & 1.88 \end{bmatrix}$$, cela signifie que le mot 1 a un score de 4.5 avec lui-même, ce qui est logique (il se comprend lui-même !). Le mot 1 a un score de 3.0 avec le mot 2, ce qui signifie qu’il y a un lien modéré entre eux. Le mot 1 a un score de 2.5 avec le mot 3, donc il est moins pertinent par rapport au mot 3. Le mot 2 fait plus attention au mot 1 (3.15) qu’au mot 3 (1.6).

Les matrices de poids, W_Q et W_K, sont appliquées à l’embedding initial de chaque mot. Elles sont apprises au cours de l’entraînement : les poids d’attention sont ajustés pour améliorer la prédiction que fait le LLM du prochain mot. Chaque matrice de poids est entraînée séparément par descente de gradient ; elles appartiennent à des couches distinctes du réseau de neurones. C’est une méthode d’optimisation, sans l’intervention d’aucune théorie sous-jacente. En résumé :

1️⃣ Le modèle fait une prédiction : il génère du texte ou répond à une question.
2️⃣ On compare cette sortie avec le texte réel des données d’entraînement.
3️⃣ On calcule une erreur avec une fonction de perte (ex: cross-entropy).
4️⃣ On ajuste les poids dans les matrices pour minimiser cette erreur.

La formule d’attention est la suivante : $$\text{Poids d’attention}(Q,K,V) = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) V$$ où V est l’embedding non modifié des mots, qui contient donc les informations réelles. Q et K servent uniquement à décider « quel mot regarder » et V contient l’information réelle du mot, et n’est utilisée qu’une fois la sélection faite. Le mécanisme d’attention ne modifie pas V, il ne fait que combiner optimalement les informations réelles contenues.

Plusieurs matrices d’attention sont calculées en parallèle, permettant de saisir différentes facettes du contexte simultanément : c’est l’attention dite multi-tête.

Concepts clés des LLM

En résumé, un LLM repose sur les concepts suivants, dont certains seront mis en pratique dans la section suivante :
La tokenisation : découpage du texte en unités traitables (mots ou sous-mots).
L’embedding : transformation des mots en vecteurs de nombres réels.
Les réseaux de neurones récurrents (RNN)
Les transformeurs : mécanisme d’auto-attention pour capturer les relations entre mots.
La génération de texte : calcul des probabilités et sélection du mot le plus probable.

Un LLM, avec réseau neuronal récurrent (ancienne génération) expliqué en code basique (Python)

Ce code présente un LLM d’ancienne génération qui utilise un réseau de neurone récurrent (RNN) qui était utilisé avant l’apparition des transformeurs. Il s’agit seulement d’appréhender les mécanismes et les concepts évoqués (token, embedding) à travers un exemple.

Librairies Pytorch

On importe les librairies nécessaires dans Python. PyTorch permet de manipuler des tenseurs et de créer des modèles de deep learning.
– torch.nn contient toutes les classes de réseaux de neurones (ex: nn.Linear, nn.ReLU).
– torch.optim contient les algorithmes d’optimisation (ex: Adam, SGD).

 import torch
 import torch.nn as nn
 import torch.optim as optim

Données d’entraînement

On fournit ensuite les données d’entraînement sous formes de phrases simplifiées. Le LLM va apprendre les relations implicites entre les mots de façon à pouvoir former tout seul des phrases cohérentes.

corpus = [
    "oem fournit des informations utiles",
    "chatgpt est efficace",
    "les ia vont augmenter la productivite",
    "des emplois seront detruits dans certaines regions",
    "certains secteurs sont plus menaces par les ia",
    "chatgpt est un ami de longue date"
]

On crée une liste qu’on appelle corpus qui contient chacune de ses phrases. Chaque élément de cette liste est une phrase.

Tokenisation simplifiée

On attribue un indice unique à chaque mot et on crée un dictionnaire bidirectionnel.

vocab = sorted(set(" ".join(corpus).split()))
word_to_idx = {word: i for i, word in enumerate(vocab, start=1)}
word_to_idx["<PAD>"] = 0

Tous les mots en lettre sont les clés du dictionnaire appelé word_to_idx et les valeurs sont les nombres attribués à chacun d’entre eux. Par exemple la clé « ami » a pour valeur 1. On accède à la valeur 1 en appelant : word_to_idx[« ami »] qui renvoie donc 1. On utilise un token spécial, <PAD> pour les 0, qui sera ignoré dans les calculs d’apprentissage.

idx_to_word = {i: word for word, i in word_to_idx.items()}

On crée le dictionnaire inverse où les clés sont les nombres et les valeurs les mots en lettre. idx_to_word[1] renvoie ‘ami’.

vocab_size = len(word_to_idx)

On crée une variable qui contient le nombre d’éléments de notre liste et donc le nombre de mots contenus dans nos données d’entraînement, auquel on ajoute l’indice 0 utilisé plus tard. Soit ici 33 mots + l’indice 0.
Exemple :

print(word_to_idx["ami"])  # Retourne un indice unique
print(idx_to_word[0])  # Retourne le mot correspondant à l'indice 1

Création des données : entrée = mots précédents, sortie = mot suivant

Le but du LLM est d’apprendre à prédire le mot suivant à partir des mots précédents. On va donc structurer les données de cette façon : le LLM connaît les n-1 mots précédents et il doit trouver le n-ième mot, celui qui a la probabilité la plus forte d’apparaître après les n-1 qu’il connaît.
Chaque phrase va être divisée en deux éléments : un contexte, la liste des indices des mots précédents, et l’indice du mot suivant. Ces deux éléments seront stockés dans une liste qu’on appelle data. Chaque phrase est donc convertie en une séquence d’indices utilisable par le modèle.

def tokenize_sentence(sentence):
    return [word_to_idx.get(word, word_to_idx["<PAD>"]) for word in sentence.split()]

On définit une fonction qu’on appelle tokenize_sentence qui prend une phrase composée de mots en lettre et la convertit en une liste d’indice, en utilisant le dictionnaire word_to_idx (qui pour chaque mot en lettre nous retourne un nombre).
On a ajouté une gestion des mots inconnus (qui ne figurent pas dans notre dictionnaire) : au lieu de renvoyer une erreur, les mots inconnus seront remplacés par <PAD>.
Par exemple :

tokenize_sentence('oem fournit des informations utiles') #retourne [20, 13, 8, 15, 29]. 

data = []
for sentence in corpus:
    tokens = tokenize_sentence(sentence)
    for i in range(1, len(tokens)):
        data.append((tokens[:i], tokens[i]))

On crée notre liste data. Chaque élément est une paire :
tokens[:i] → Liste d’indices représentant les mots précédents (contexte).
tokens[i] → Indice du mot suivant à prédire.

Voici les 4 premiers éléments de data :
([20], 13),
([20, 13], 8),
([20, 13, 8], 15),
([20, 13, 8, 15], 29)
Ils correspondent à la première phrase « oem fournit des informations utiles » ou [20, 13, 8, 15, 29] en indices. Le LLM va donc s’entraîner à prédire chaque mot, en plusieurs étapes : le 2ème, puis le 3ème, le 4ème et enfin le 5ème. 5 mots donc 4 étapes, soit 4 contextes.

Dans la boucle qui crée la liste data, chaque phrase de la liste corpus est traitée. Ensuite pour chaque phrase, on crée successivement les paires contexte / mots à prédire, avec i de 1 jusqu’à la longueur maximale de notre phrase, ici 5. tokens[:i] afficher les i premiers éléments d’une liste et tokens[i] le ième. Comme le premier indice est 0, on obtient bien les n-1 premiers mot et le n_ième, à prédire.
En prenant toujours pour exemple la phrase « oem fournit des informations utiles » et pour le premier passage dans la bouche on a tokens[:1] retourne bien 20 ( contexte, ici l’indice d’un seul mot, le premier) et l’indice du mot suivant à prédire : 13.

Encodage données pour Pytorch

Nous allons maintenant créer ce qu’on entre dans le LLM, X_train, donc le contexte, et ce qu’il en sort, y_train, sa prédiction. L’objectif sera de réduire l’erreur commise par le modèle entre sa prédiction y_train et le mot réellement utilisé dans la phrase des données d’entraînement.

X_train va contenir tous les contextes : les premiers mots de chaque séquence à partir desquels le LLM doit prédire le mot suivant et y_train va contenir les mots à prédire.

Pour utiliser Pytorch, on a besoin de préparer les données d’une certaine façon. Jusqu’ici nous avions des listes que nous allons maintenant transformer en tenseurs. Pourquoi ? Un tenseur est un tableau multidimensionnel (généralisation des vecteurs/matrices) qui représente des données de manière uniforme. PyTorch les utilise car ils permettent d’exécuter rapidement des opérations vectorisées (notamment sur GPU), ce qui est bien plus efficace que la manipulation de simples listes Python.

max_train_len = max(len(tokens) for tokens, _ in data) #longueur maximales des séquences d'entraînement
def pad_sequence(seq, max_len):
    return seq[:max_len] + [0] * max(0, max_len - len(seq))

Les phrases ont des longueurs (nombre de mots) différentes donc ici on comble les trous des phrases plus courtes en ajoutant des zéros à la fin de la séquence (« padding ») pour avoir des longueurs uniformes.

X_train = torch.tensor([pad_sequence(tokens, max_train_len) for tokens, _ in data])

X_train contient tous les contextes : les premiers mots de chaque séquence à partir desquels le LLM doit prédire le mot suivant et y_train va contenir les mots à prédire. torch.tensor([…]) convertit ici la liste (de listes) en un tenseur 2D (une matrice est un tenseur 2D). Avant la conversion, on a une liste de séquences. torch.tensor() assemble toutes ces séquences en un seul objet de type torch.
On obtient in fine une ligne par contexte de phrases.

y_train = torch.tensor([target for _, target in data])

y_train récupère uniquement les cibles = les mots à prédire. Si chaque phrase a N mots, elle génère N-1 entrées.
Dans la syntaxe for _, target in data, le symbole _ est une simple convention indiquant « on ne se sert pas de cette variable ». Python parcourt chaque tuple de data et attribue la première valeur du tuple à _ (qui sera ignorée) et la deuxième valeur à target. Chaque entrée de data est un couple(contexte, cible). Quand on écrit [target for _, target in data], on extrait simplement la deuxième valeur, c’est-à-dire le mot à prédire.

Définition du mini LLM

On définit une classe qu’on appelle MiniLLM, composée d’une méthode (une fonction) qu’on appelle forward. On les appellera plus tard : on générera alors des instances particulières de notre LLM.

class MiniLLM(nn.Module):
    def __init__(self, vocab_size, embedding_dim=10, hidden_dim=20):
        super(MiniLLM, self).__init__()
        self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=0)
        self.rnn = nn.RNN(embedding_dim, hidden_dim, batch_first=True)
        self.fc = nn.Linear(hidden_dim, vocab_size)

    def forward(self, x):
    x = self.embedding(x)
    output, _ = self.rnn(x)
    out = self.fc(output[:, -1, :])  # Prendre la dernière sortie du RNN
    return out

Commençons avec le plongement lexical (ou embedding) :

nn.Embedding(vocab_size, embedding_dim)

Jusqu’ici, nos phrases étaient exprimées sous forme d’une suite d’indices (à chaque mot était attribué un indice : revoir l’étape de création des dictionnaires). Le but du LLM est de comprendre la relation entre les mots, ce qui n’est pas facile à effectuer avec des indices arbitraires et discrets. Avec un embedding, chaque mot est transformé en un vecteur continu. Cela permet de capturer des relations entre les mots : les mots proches en signification auront des vecteurs proches. On a plus de flexibilité qu’avec de simples indices.
Sans embedding : [0, 1, 2] (indices),
Avec embedding : [0.12, -0.4, 0.9] (vecteurs continus).
Après cette étapes, un réseau récurrent de neuronne (RNN) est appliqué à cette nouvelle séquence, non plus d’indices, mais de vecteurs :

nn.RNN(embedding_dim, hidden_dim, batch_first=True)

Au sein de la couche cachée, le RNN minimise une fonction de perte pour mettre à jour correctement son état caché h_t et améliorer la prédiction y_t.
$$h_t=f(W_h x_t + U_h h_{t−1}+ b_h)$$

$$y_t=g(W_y h_t+b_y)$$

Les W​ sont des matrices de poids à apprendre, b_h, b_y​ sont des biais. $$\theta = \{ W_h, U_h, W_y, b_h, b_y \}$$ représente l’ensemble des paramètres du réseau de neurones que l’on cherche à optimiser. La fonction de perte indique l’erreur commise entre la prédiction et la réalité de la sortie y_t. Sur la séquence de temps t, elle s’écrit : $$ L = \sum_{t=1}^{T} \text{Loss}(y_t, \hat{y}_t)$$. Après chaque prédiction, le modèle ajuste ses poids pour mieux prédire à la prochaine étape. Ce processus, appelé descente de gradient, suit une règle simple : il modifie les poids dans la direction qui réduit l’erreur : $$\theta \leftarrow \theta – \eta \frac{\partial L}{\partial \theta}$$
1️⃣ Le modèle fait une prédiction.
2️⃣ On calcule l’erreur grâce à la fonction de perte.
3️⃣ On ajuste les poids dans la direction qui réduit l’erreur. C’est la dérivée de la perte par rapport aux poids qui indique la direction à suivre.

n.Linear

Cette étape applique une transformation linéaire à la sortie du RNN, qui est en logit. Une fonction d’activation telle que softmax est souvent utilisée ensuite pour transformer ces valeurs en probabilités sur le vocabulaire.

Initialisation

model = MiniLLM(vocab_size)

Cette ligne crée une instance du modèle MiniLLM qu’on appelle model, avec un vocabulaire de taille vocab_size, donc le nombre de mots, dans notre cas 37.

criterion = nn.CrossEntropyLoss()

Cette ligne définit la fonction de perte utilisée pour entraîner le modèle. nn.CrossEntropyLoss() est la perte d’entropie croisée. Elle compare la distribution de probabilités prédite par le modèle avec la véritable classe cible et pénalise les mauvaises prédictions.

optimizer = optim.Adam(model.parameters(), lr=0.01)

cette ligne initialise l’optimiseur qui ajuste les poids du modèle en fonction de la perte calculée. l_r=0.01 est le taux d’apprentissage :
-Une valeur élevée accélère l’apprentissage mais peut être instable.
-Une valeur faible rend l’apprentissage plus précis mais plus lent.

Entraînement de l’instance model de MiniLLM

n_epochs = 500
for epoch in range(n_epochs):
    optimizer.zero_grad()
    y_pred = model(X_train)
    loss = criterion(y_pred, y_train)
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(f"Époque {epoch}, Perte: {loss.item():.4f}") 

Cette boucle d’entraînement effectue 500 itérations (époques) du processus de minimisation de la perte. Ce qui évolue au fil des époques, c’est l’état interne du modèle, notamment les poids des couches, qui sont mis à jour après chaque itération grâce à la descente de gradient. Dans cette boucle, chaque itération de l’entraînement repart toujours de zéro avec les mêmes entrées (X_train), et le modèle s’améliore uniquement parce que ses poids évoluent au fil des itérations. (La sortie y_pred ne sert pas d’entrée pour l’époque suivante, mais l’amélioration du modèle au fil des itérations fait que y_pred devient de plus en plus précis.)

y_pred = model(X_train)

Le modèle (MiniLLM) fait une prédiction sur X_train.

loss = criterion(y_pred, y_train)

La perte est calculée à l’aide de la fonction de coût (criterion), qui mesure l’écart entre y_pred (prédictions) et y_train (valeurs réelles).

loss.backward()

backward() calcule le gradient de la perte par rapport à tous les poids du modèle. Ces gradients serviront à ajuster les poids du modèle pour minimiser l’erreur.

optimizer.step()

optimizer.step() met à jour ces poids, ce qui modifie la façon dont le modèle model(X_train) produit ses prédictions y_pred à la prochaine époque, en suivant la direction qui minimise la perte. Ces étapes sont répétées 500 fois, ce qui signifie que le modèle ajuste ses poids 500 fois pour essayer de minimiser la perte et améliorer ses prédictions.

Génération de texte

def generate_text(start_text, gen_length=5):
    tokens = tokenize_sentence(start_text)
    for _ in range(gen_length):
        current_tokens = tokens[-max_train_len:]
        input_tensor = torch.tensor([pad_sequence(current_tokens, max_train_len)], dtype=torch.long)
        output_probs = model(input_tensor)
        next_word_idx = torch.argmax(output_probs[0], dim=-1).item()

        if next_word_idx == word_to_idx["<PAD>"]:
            break  # Stop si le modèle génère du padding

        tokens.append(next_word_idx)
        print("→", idx_to_word.get(next_word_idx, "<UNK>"))

Cette fonction appelle plusieurs fonctions que nous avons créées mais aussi l’instance de MiniLLM, appelée model. generate_text sert à générer du texte en utilisant le modèle entraîné.

1. Initialisation du texte de départ
start_text, c’est à dire la phrase que l’on entre dans la fonction pour prédire le dernier mot, est transformé en une liste de tokens (indices des mots dans le vocabulaire) grâce à la fonction tokenize_sentence.
Exemple : si start_text = "oem fournit des informations", les mots sont convertis en indices selon word_to_idx.

Le modèle est conçu pour prendre une séquence en entrée et prédire le mot suivant. Il ne génère pas une phrase complète en une seule étape. Au lieu de cela :
-Il prend tokens (les indices des mots déjà générés).
-Il prédit un seul mot à la fois (celui avec la probabilité la plus haute).
-Il ajoute ce mot à tokens et répète le processus jusqu’à atteindre max_train_len.

2. Boucle de génération (max_length = 5)
La boucle s’exécute gen_length fois pour générer gen_length mots supplémentaires.
À chaque itération :
1️⃣ Préparation de l’entrée
tokens est transformé en un tenseur PyTorch, après avoir été complété avec pad_sequence pour atteindre la longueur maximale attendue par le modèle (max_train_len).
(max_train_len max_train_len fixe la longueur maximale du contexte pris en compte par le modèle. Les séquences plus courtes sont complétées avec <PAD>, tandis que gen_length définit combien de nouveaux mots seront générés.)
2️⃣ Prédiction du mot suivant
Le modèle prend l’entrée et produit des probabilités (output_probs) pour chaque mot du vocabulaire.
torch.argmax(output_probs, dim=1).item() extrait l’indice du mot ayant la plus haute probabilité.
3️⃣ Ajout du mot généré
L’indice du mot généré est ajouté à tokens pour continuer la génération au tour suivant.
4️⃣ Affichage du mot généré
idx_to_word[next_word_idx] est utilisé pour retrouver le mot correspondant à l’indice et l’afficher.

generate_text("oem fournit des informations", gen_length=1) 

On obtient : « utiles » !

Un LLM, avec transformer (génération plus récente) expliqué en code basique (Python)

Commençons avec un code qui simule une étape d’attention dans un transformer. Il entraîne les matrices W_Q, W_K, W_V​ pour qu’elles améliorent la prédiction des poids d’attention. C’est donc une approche simplifiée avec une seule couche d’attention. Le but est de comprendre ce que fait la classe Pytorch nn.Transformer qui sera utilisée ensuite dans le code global de la seconde section – où plusieurs têtes d’attention seront utilisées par nn.Transformer.

Procédure d’entraînement des matrices

Nous avons une phrase de 3 mots et pour chaque mot nous avons des embeddings de dimensions 4, donc 4 caractéristiques pour chaque mot.

Cette section définit les paramètres :
– d_model indique la taille des embedding d’entrée, ici un vecteur de 4 dimensions,
– d_k définit la taille des vecteurs Q, K, et V, également un vecteur de taille 4,
– vocab_size donne le nombre de mots dans le dictionnaire,
– n_words correspond au nombre de mots dans le vocabulaire. Chaque mot aura un vecteur d’embedding.

d_model = 4
d_k = 4
vocab_size = 10
n_words = 3

On définit ensuite des matrices W_Q, W_K, W_V comme trois couches linéaires indépendantes. La classe nn.Linear(d_model, d_k, bias=False) dans PyTorch est une transformation linéaire qui applique l’opération suivante : $$ Y = X W^T$$ où X est le vecteur des embedding de taille d_model, W est la matrice que le modèle doit apprendre et Y est la prédiction du modèle. Même si aucune itération n’a encore été faite sur les poids, dès la création des couches, PyTorch initialise la matrice des poids W​ avec des valeurs aléatoires suivant une distribution uniforme : ces poids au départ aléatoires sont mis à jour au cours de l’entraînement par la technique de la descente de gradient.

W_Q = nn.Linear(d_model, d_k, bias=False)
W_K = nn.Linear(d_model, d_k, bias=False)
W_V = nn.Linear(d_model, d_k, bias=False)

On définit une fonction qui applique une transformation linéaire, qui transforme un vecteur de dimension 4 en un vecteur de dimension 10 (taille du vocabulaire).

output_layer = nn.Linear(d_k, vocab_size)

On définit, pour l’exemple, une phrase avec 3 mots, où chaque mot est un vecteur de taille 4. On définit également des valeurs cibles, le résultat vers lequel le modèle doit tendre : idéalement, si on lui entre X, on aimerait qu’il produise target. L’écart entre l’output du modèle et la cible mesurera l’erreur commise par le LLM.

X = torch.tensor([[0.1, 0.2, 0.3, 0.4],  # Mot 1
                  [0.5, 0.6, 0.7, 0.8],  # Mot 2
                  [0.9, 1.0, 1.1, 1.2]], dtype=torch.float32)  # Mot 3

On crée Q, K et V.

Q = W_Q(X)  
K = W_K(X)  
V = W_V(X)

On calcule les scores d’attention et on obtient une matrice de taille (n_words x n_words), scores, qui contient les scores bruts de similarité entre chaque mot. Ici scores est de taille 3×3. scores pourrait par exemple prendre ces valeurs :
[ 0.45, -0.15, 0.30],
[-0.20, 0.60, 0.10],
[ 0.25, 0.05, 0.50],
indiquant que la similarité brute entre le mot 1 et le mot 2, considérée du point de vue du mot 1 est -0.15, mais qu’elle est de -0.20 considérée du point de vue du mot 2. Le mot « chien » accordera peut-etre plus d’importance au mot « os », que le mot « os » au mot « chien » (qui peut se rapporter à l’homme dans un contexte médical, à de nombreux animaux etc.). L’attention est asymétrique.

scores = torch.matmul(Q, K.T) / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))

Ensuite, on transforme les scores en probabilités (1ère ligne), de façon à ce que chaque ligne somme à 1. attention_weights pourrait par exemple ressembler à :
[0.306, 0.321, 0.373],
[0.289, 0.391, 0.320],
[0.315, 0.300, 0.385]
Chaque ligne indique la distribution d’attention, la proportion d’importance accordée par chaque mot aux autres : le mot 3 doit accorder 31,5% de son attention au mot 1, 30% au mot 2 et 38,5% à lui-même.
Puis ces poids sont multipliés par V (2ème ligne). On obtient alors output qui est une nouvelle représentation de chaque mot qui agrége les informations V pondérées par l’attention. C’est le nouvel embedding contextualisé, enrichi par le contexte de chaque mot : l’embedding intégre désormais les informations venant de chaque mot grâce au mécanisme d’attention. Par exemple, output pourrait être :
[1.0536, 1.2536, 1.4536, 1.6536],
[1.0248, 1.2248, 1.4248, 1.6248],
[1.0560, 1.2560, 1.4560, 1.6560]
Chaque ligne est le nouvel embedding de chaque mot, et chaque colonne une caractéristique, une dimension de sa répresentation.
Enfin, ces embedding sont convertis en vecteurs de logit sur le vocabulaire, qui contient 10 mots (3ème ligne). output_vocab sera de la forme :
[ 0.2, -1.3, 0.8, 2.1, -0.5, 1.0, 0.3, -0.7, 1.5, 0.9],
[ 0.1, -0.9, 0.5, 1.8, -0.4, 0.7, 0.2, -0.5, 1.2, 0.8],
[ 0.3, -1.0, 0.9, 2.0, -0.6, 1.1, 0.4, -0.8, 1.7, 1.0]
Chaque ligne correspond à la distribution de logits sur les 10 mots de vocabulaire pour chacun des 3 mots de la phrase. La première ligne donne la vraisemblance que le mot 1 de la phrase de 3 mots soit suivi des 10 mots du vocabulaires (en colonne). (En appliquant une fonction softmax, on obtiendrait des probabilités mais ce n’est pas fait ici car la fonction de minimisation de perte nn.CrossEntropyLoss attend des logits non normalisés et applique log_softmax en interne).

attention_weights = torch.softmax(scores, dim=-1) #scores de similarité
output = torch.matmul(attention_weights, V) #nouvel embedding contextualisé
output_vocab = output_layer(output)

On crée une cible, celle que le modèle doit atteindre, sous forme d’indice des mots attendus.

target = torch.tensor([2, 5, 8], dtype=torch.long) 

On calcule ensuite la perte avec une fonction de perte, l’erreur quadratique moyenne, sur la prédiction de mots (et non sur les poids qu’on ne connaît bien sûr pas – on n’a pas de « cible » pour eux). nn.CrossEntropyLoss() est la classe la plus appropriée, car elle est conçue pour des problèmes de classification comme la prédiction du mot suivant. Ce qu’elle va faire : comparer argmax(output_vocab), soit le mot identifié comme le plus probable, avec target, le mot attendu.

loss_fn = nn.CrossEntropyLoss()
loss = loss_fn(output_vocab, target)

On définit l’optimiseur Adam qui met à jour les poids des matrices W_Q, W_K, et W_V à un taux d’apprentissage, la vitesse de mise à jour des poids lr=0.01.

optimizer = optim.Adam(
    list(W_Q.parameters()) + list(W_K.parameters()) + list(W_V.parameters()) + list(output_layer.parameters()),
    lr=0.01
)

Enfin, on calcule le gradient de la fonction de perte par rapport aux 3 matrice W et on utilise l’optimiseur pour réduire l’erreur à la prochaine itération.

loss.backward()
optimizer.step()

Ce code très simplifié permet de comprendre une opération effectuée dans le code ci-dessous par une classe de Pytorch que l’on appellera, nn.Transformer.

Mini LLM avec transformateur

Le début du code est très semblable à celui étudié dans le cas des RNN : créations des dictionnaires, tokenisation, padding.

import torch
import torch.nn as nn
import torch.optim as optim

corpus = [
    "oem fournit des informations utiles",
    "chatgpt est efficace",
    "les ia vont augmenter la productivite",
    "des emplois seront detruits dans certaines regions",
    "certains secteurs sont plus menaces par les ia",
    "chatgpt est un ami de longue date"
]

vocab = sorted(set(" ".join(corpus).split()))
word_to_idx = {word: i for i, word in enumerate(vocab, start=1)}
word_to_idx["<PAD>"] = 0  # Token de padding

idx_to_word = {i: word for word, i in word_to_idx.items()}
vocab_size = len(word_to_idx)

def tokenize_sentence(sentence):
    return [word_to_idx.get(word, word_to_idx["<PAD>"]) for word in sentence.split()]

data = []
for sentence in corpus:
    tokens = tokenize_sentence(sentence)
    for i in range(1, len(tokens)):
        data.append((tokens[:i], tokens[i]))

max_train_len = max(len(tokens) for tokens, _ in data)

def pad_sequence(seq, max_len):
    return seq[:max_len] + [0] * max(0, max_len - len(seq))

X_train = torch.tensor([pad_sequence(tokens, max_train_len) for tokens, _ in data])
y_train = torch.tensor([target for _, target in data])

Mais ensuite le modèle est basé sur un transformateur et non un réseau de neurones récurrent :

class MiniTransformerLLM(nn.Module):
    def __init__(self, vocab_size, embedding_dim=32, num_heads=2, hidden_dim=64, num_layers=2):
        super(MiniTransformerLLM, self).__init__()
        self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=0)
        self.positional_encoding = nn.Parameter(torch.zeros(1, max_train_len, embedding_dim))
        self.transformer = nn.Transformer(
            d_model=embedding_dim, 
            nhead=num_heads, 
            num_encoder_layers=num_layers, 
            num_decoder_layers=num_layers,
            dim_feedforward=hidden_dim,
            batch_first=True
        )
        self.fc = nn.Linear(embedding_dim, vocab_size)

    def forward(self, x):
        x = self.embedding(x) + self.positional_encoding[:, :x.size(1), :] 
        tgt = x[:, -1:, :]
        out = self.transformer(x, tgt)
        return self.fc(out[:, -1, :]) 

Cette classe MiniTransformerLLM appelle non pas nn.RNN (réseau neuronal récurrent) mais nn.Transformer.

A noter : on présente ici une utilisation très simplifiée du module nn.Transformer.

nn.Transformer implémente un mécanisme très proche du code de la section précédente mais avec plusieurs couches, et plusieurs têtes d’attention. En effet, une seule attention ne peut pas capturer toutes les relations entre les mots. En effet, un mot peut être important pour plusieurs raisons différentes (ex: syntaxe, sémantique, lien avec d’autres phrases). Le modèle utilise alors plusieurs têtes d’attention en parallèle. Il divise les Q, K et V en plusieurs sous-espaces. Chaque sous-espace a sa propre matrice.

Les paramètres clés sont :
vocab_size → Nombre total de mots dans le vocabulaire.
embedding_dim → Taille des vecteurs qui représentent les mots.
num_heads → Nombre de têtes d’attention (multi-head attention).
hidden_dim → Taille de la couche dans chaque bloc du transformeur.
num_layers → Nombre de couches d’encodeur et de décodeur.

self.embedding convertit les mots en vecteurs d’embedding plutôt qu’en simple entier. On réserve l’indice 0 pour le padding (les mots vides dans les séquences de taille variable).

#Initialisation et entraînement
model = MiniTransformerLLM(vocab_size)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)

n_epochs = 500
for epoch in range(n_epochs):
    optimizer.zero_grad()
    y_pred = model(X_train)
    loss = criterion(y_pred, y_train)
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(f"Époque {epoch}, Perte: {loss.item():.4f}")

#Fonction de génération de texte
def generate_text(start_text, gen_length=5):
    tokens = tokenize_sentence(start_text)
    for _ in range(gen_length):
        current_tokens = tokens[-max_train_len:]
        input_tensor = torch.tensor([pad_sequence(current_tokens, max_train_len)], dtype=torch.long)
        output_probs = model(input_tensor)
        next_word_idx = torch.argmax(output_probs[0], dim=-1).item()

        if next_word_idx == word_to_idx["<PAD>"]:
            break  # Stop si le modèle génère du padding

        tokens.append(next_word_idx)
        print("→", idx_to_word.get(next_word_idx, "<UNK>"))

generate_text("oem fournit des informations", gen_length=1)

Le modèle est ensuite initialisé et entraîné comme vu précédemment. En particulier, les lignes :

    y_pred = model(X_train)
    loss = criterion(y_pred, y_train)
    loss.backward()
    optimizer.step()

forment l’itération d’entraînement du réseau de neurone.
1️⃣ y_pred = model(X_train) : les données d’entrée (X_train) sont passée dans le modèle qui sont transformées en une prédiction (la probabilité pour chaque mot).
2️⃣ loss = criterion(y_pred, y_train) : la fonction de perte compare la prédiction y_pred avec la probabilité attendu y_train. Cette comparaison génère une valeur numérique, qui évalue la performance du modèle.
3️⃣ loss.backward() : les dérivées partielles de la perte par rapport à chacun des poids est calculée et ces gradients sont ensuite stockés dans .grad. Ils indiquent comment les poids doivent être modifiés pour réduire la perte.
4️⃣ L’optimiseur (Adam ici) utilise les gradients calculés pour mettre à jour les poids du modèle de cette façon : parametre←parametre−η×gradient.

La bouche d’entraînement est ici exécutée 500 fois : 500 itérations ou époques (n_epochs = 500).